「我交過幾個男/女友,還想再試試其他人,最終我都要定下來,但是在什麼時候呢?」
我想大家都可能看過以下這個故事;
柏拉圖有一天問老師蘇格拉底什麼是愛情?蘇格拉底叫他到麥田走一次,要不回頭地走,在途中要摘一棵最大最好的麥穗,但只可以摘一次。
柏拉圖覺得很容易,充滿信心地出去,誰知過了半天他仍沒有回去,最後,他垂頭喪氣出來在老師跟前訴說空手而回的原因:“很難得看見一株看似不錯的,卻不知是不是最好,不得已,因為只可以摘一次,只好放棄,再看看有沒有更好的,到發現已經走到盡頭時,才發覺手上一棵麥穗也沒有。”
這時,蘇格拉底告訴他:“那就是愛情” 雖然不能一概而論,但愛情的確與這很像。因為人總以為會有更好,但這樣說我昰不能去追求更好的嗎?
可以一個「最適實驗理論」(optimal experimentation theory) 為開端和大家討論。
在近代,這個問題稱為秘書問題,或者最優停止問題,它是在1950年左右由密西根大學的梅裡爾•弗拉德(Merrill M. Flood)提出的,在1960年美國最著名的科普數學家馬丁•伽德納(Martin Gardner)在《美國科學人》雜誌自己的專欄“趣味數學”中刊登了這個問題。
“假設一堆人申請一個秘書崗位,而你是面試官,你的目標是從這堆申請人中遴選出最佳人選。你可以輕鬆地判斷哪一名申請人更加優秀。按照隨機順序,每次面試一名申請人。你隨時可以決定將這份工作交給其中一人,而對方只能接受,於是面試工作就此結束,後面的人就沒有機會了。但是,一旦你否決其中一名申請人,就不能改變主意再回頭選擇他。究竟採取一個什麼策略才能使得我們有最大的可能找到最佳人選呢?“
比如有100個秘書應聘,一般人都不會接受第一個應聘的秘書,無論他有多優秀。因為從概率上講,他在100個人中最優秀的概率只有1%。我們會考察第一個人,但是依然會拒絕他,並把他的水準作為參考。小防盜:本文來源自hzone18.com
如果我們考察了30個人,找到最優秀的人概率為30%,但是走到這一步的前提是這30%的人都被你拒絕了。我們考察的人越多,就越瞭解應聘者,但是可供我們選擇的人也越來越少了。
如果我們考察完全部100個人,我們就有100%的概率知道哪一個人是最優秀的,但是這樣做的代價就是放棄了所有人,我們一無所得。
最優解的前題是對方一定會接受你(你一定是他想要的) 或只考慮已經在交往的情況。
無論是蘇格拉底的故事,還是秘書問題,它們的本質都是相同的。我們要在有限個體中找到最優的一個,但是一旦放棄(離開找下一個)就不能回頭。馬丁加德納提出:我們應該而且也只能選擇這樣的策略:
在考察最初的幾個人時,無論他們多優秀,都拒絕他們,他們就構成了樣本區。我們拒絕了樣本區裡的人,但是並非一無所獲:我們已經瞭解了候選人/備選者的大體水準。小防盜:本文來源自hzone18.com
從樣本區後面的第一個人開始,假如這個人比樣本裡所有的人都優秀,我們就接受他。如果他沒有樣本裡最優秀的人優秀,我們就拒絕他,繼續考察下一個人。
假如所有的人都考察完了,那麼我們被迫選擇最後一個,因為再不選就會一無所獲。這恰好對應了女生在年齡增長到一定程度後會找一個主觀上沒有比較好的對像。
如下圖:
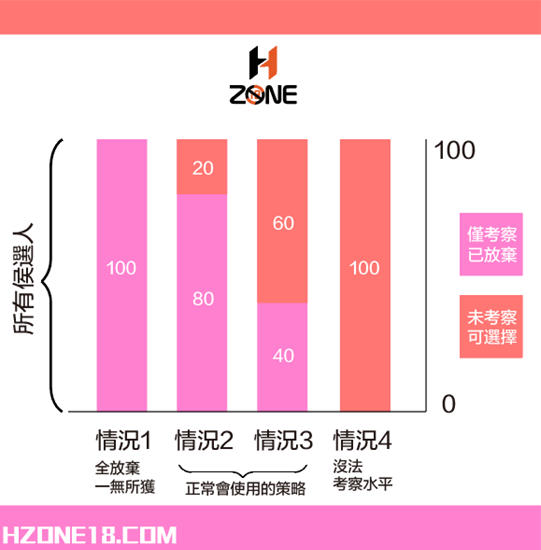
緊接著的問題就是:考察的樣本應該有多少,才有最大的可能找到最優秀的那個人呢?
不想看數學模型的可跳過這部分:
從最簡單的情況開始。假設一個女生(男生也適用)一生中只會談1次戀愛,那麼情況就非常簡單了,和對像結婚,否則女生將一無所獲。此時女生找到真命天子的概率是100%。小小防盜:本文來源自hzone18. com
如果女生一生可以談兩次戀愛,那麼她面臨兩個選擇:與第一個人結婚。或者與第一個人分手,與第二個人結婚。因為這兩個人誰更優秀是隨機的,因此無論採用哪種策略,女生獲得真命天子的概率都是50%,這種情況下只能碰運氣了。
如果女生一生會戀愛三次,那麼情況就變得有趣了。如果這三個戀愛者按順序分別是A、B、C,三個人的優秀指數用1、2、3表示,其中3是最優秀的人。但是女生並不清楚三個人中誰是指數為3的人,她該怎麼辦呢?下圖為可能的組合:
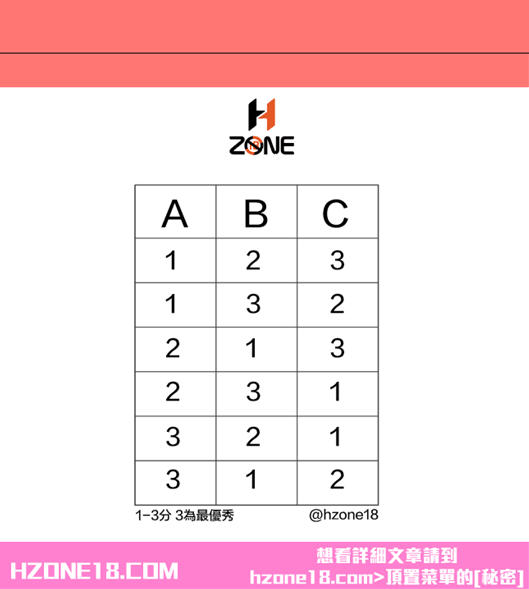
按照前面所說的策略,女生應該劃定幾個人作為樣本區,考察他們,並從樣本後面的備選區選擇終身伴侶。
如果女生的樣本個數是0,就表示女神會和第一個男朋友A結婚,在全部六種可能中,第一個人最優秀(指數為3)的可能有2種,因此女生找到真命天子的概率是2/6=33%。如下圖所示。
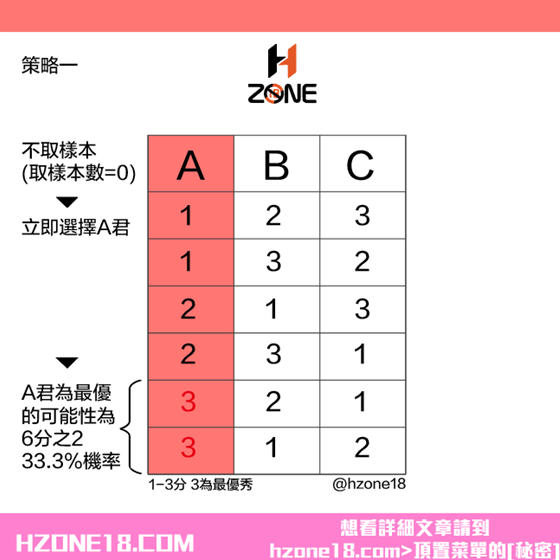
如果女生的樣本個數是1,就表示女生會把男朋友A作為樣本,作為考察組並拒絕他。在B和C中選擇自己的終身伴侶,前提是要比A優秀。在這種情況下,女神有三次會找到最優秀的(指數為3),找到最優秀的人概率為3/6=50%。注意到最後兩種情況,由於最優秀的人落在了樣本區間,女神被迫選擇最後一個人。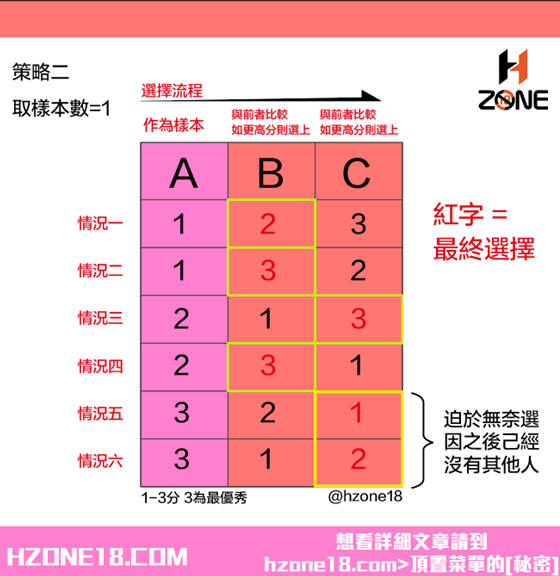
如果女生的樣本個數為2,就是前兩個人A和B作為樣本,於是女生只能選擇第三個人C。此時女生有兩種可能選擇到最優秀的(指數為3的)人,找到最優解的概率為2/6=33%。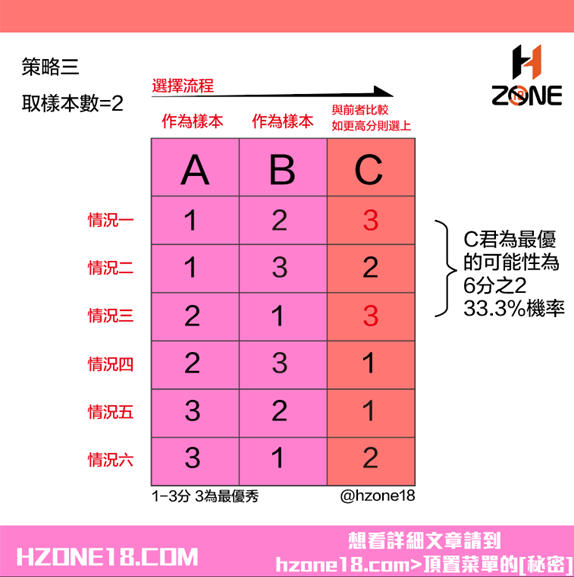
綜上所述,當女生預計自己會談三場戀愛時,選擇第一個人作為樣本是最好的方法,她會有50%的概率找到自己的真命天子——那個最優秀的人。
如果女生會談5場、6場或者7場戀愛,情況又是如何呢?時間關係我們已經計算出樣本個數的最優解,以及在這樣的策略下找到真命天子(女)的概率。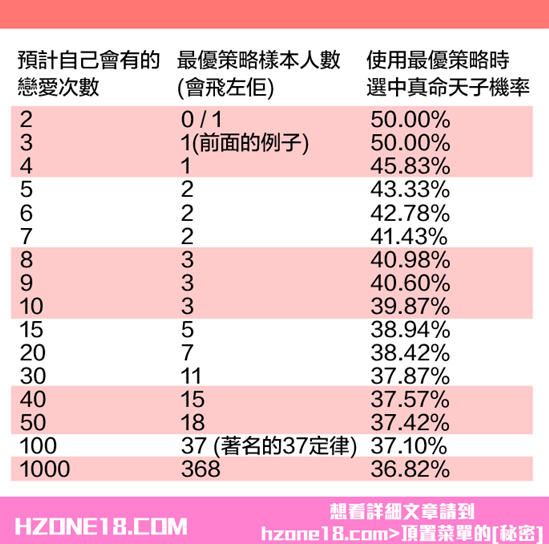
我們會發現,如果女生預計戀愛十次,就應該把前面3個人當作樣本,這樣她有39.87%的概率找到最優秀的伴侶。如果女生戀愛100次,就應該把前37個人當作樣本,找到最佳伴侶的概率為37.1%。如果女生戀愛1000次,就應該把前面368個人當作樣本,她有36.82%的概率找到最好的人。在1000個人中找到最好的,居然還有三分之一以上的概率,這個方法簡直逆天了!小小防盜:本文來源自hzone18. com
詳細的數學模型
我們先定一個目標,這輩子最多和 n 個人談戀愛。先和前面幾個見面,看看整體素質怎麼樣,從數學模型上說,就是先試前面 k 個人,不管這些人有多好(做個渣男/女);然後從第 k+1個人開始,一旦看到比之前所有人都要好的人,就毫不猶豫地選擇她。不難看出, k 的取值很講究,太小了達不到試的效果,太大了又會導致真正可選的餘地不多了。這就變成了一個純數學問題:在 n 已知的情況下,當 k 等於何值時,按上述策略選中最佳伴侶的概率最大?假設最適合你的人出現在了第 i 個位置上, 選中最佳伴侶的概率為 P(k) ,選中的第 i 個伴侶意味著前面 i−1 個人中最好的人出現在前 k 個人裡。這個概率是 k/(i−1),如下圖所示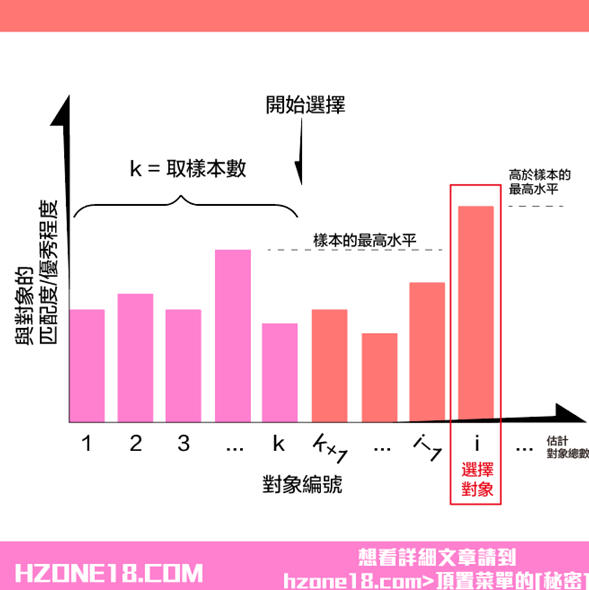

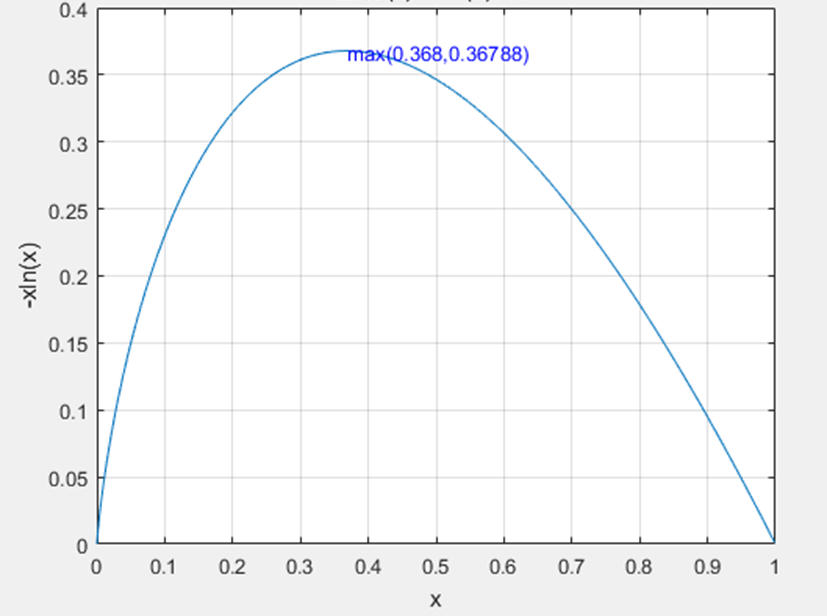
結論,如果你預計伴侶有 n 個人(n為無窮大),你應該先拒絕掉前 n/e 個人,靜候下一個比這些人都好的人。假設你一共會遇到大概 30 個伴侶,就應該拒絕掉前 30/e ≈ 30/2.718 ≈ 11 個,然後從第 12 個開始,一旦發現比前面 11 個求愛者/伴侶都好的人,就果斷接受他。由於 1/e 大約等於 37%,因此這條法則也叫做 37% 法則。上述說法有個問題,老實說我們一輩子也不會遇到無窮多個異性,所以37%這個值太高了,經過多次模擬發現,如果一生考慮交往的伴侶數量 n 在[3到100]這個區間的話,我們應該選擇拒絕掉前1/3的伴侶,1/3這個數好記又方便,算出來的值也會更加準確。
上面這個模型有一點不完善的地方是,如果前面遇到的幾個對象中存在一生摯愛,後面遇到的人永遠無法超越前面幾個,那豈不是要孤獨終老了!
按照上述模型,如果我們拋棄掉前1/3的伴侶,一旦最好的出現在前1/3裡面,意味著我們今後將孤獨終老。模型不完整,缺少了必要假設導致我們有1/3的概率孤獨終老。小小防盜:本文來源自hzone18. com
為了避免情感悲劇模型二出現了
用兩個假設將模型補充完整:

以上所說,無非都是一種市場調查,不止在愛情中用到,在商場或學業上也能應用。很多人說,自己的緣份未到,但其實是自己沒有把握住。
如果一年年過去,你要的人還沒出現,你就要有概念,你係在圖表中的那一個階段,你要更大幅度地降低標準。例如:你可以設定30歲前(類似定k值為界線)都不太降低標準。30歲後遇到質素到前30%(下調參數 l )就可以接受。以上說了這麼多,都需要符合一個前題,就是預先已經知道一生中能遇到的人或能談的戀愛的數目,但我們不是在打機/電動,不可能以第三者角度去看自己人生,也許之後的人才是真愛,所以或多或少都存在冒險成分,但人生何嘗不是一場冒險呢!
再以故事收尾,柏拉圖有一天又問老師蘇格拉底什麼是婚姻?
蘇格拉底叫他到彬樹林走一次,要不回頭地走,在途中要取一棵最好、最適合用來當聖誕樹用的樹材,但只可以取一次。
柏拉圖有了上回的教訓,充滿信心地出去,半天之後,他一身疲憊地拖了一棵看起來直挺、翠綠,卻有點稀疏的杉樹。小小防盜:本文來源自hzone18. com
蘇格拉底問他:“這就是最好的樹材嗎?”
柏拉圖回答老師:“因為只可以取一棵,好不容易看見一棵看似不錯的又發現時間、體力已經快不夠用了,也不管是不是最好的,所以就拿回來了。”
這時,蘇格拉底告訴他:“那就是婚姻”
真理一定藏在這裡,可能在第一段,也可能在中間,也可能在最後一句。也是說其實我寫了什麼對你而言毫不重要,重要的是你有在做自己的思考,與我的文章對話、與自己對話,你會發現我寫什麼不重要,到那時你就會產生名為智慧的果實了。
